介绍

方差分析（analysis of variance，ANOVA）是英国统计学家R.A.Fisher提出的对两个或多个样本均值差异显著性检验的方法。它的基本思想是将测量数据的总变异按照变异来源分解为处理（组间）效应和误差（组内）效应，并作出其数量估计，从而确定试验处理对研究结果影响力的大小。

在一个实验中可以得出一系列不同的观测数据，造成观测值不同的原因可能如下：

• 处理效应（treatment effect），由于处理因素不同引起的
• 误差效应（error effect），由于实验过程中偶然性因素的干扰和测量误差所致

方差分析主要有以下几种：

• 单因素方差分析（one-way ANOVA）
• 二因素方差分析（two-way ANOVA）
• 混合方差分析（mixed ANOVA）
• 重复测量方差分析（repeated measures ANOVA）

本文只介绍单因素方差分析(one-way ANOVA)，在下文中均称为方差分析(ANOVA)。

数据

示例数据为 palmerpenguins包中的 penguins数据：

# install.packages("palmerpenguins")
library(palmerpenguins)

该数据集中包含344只三种企鹅（Adelie，chinstrap和Gentoo）的八项观测数据，在本文中只保留鳍长（flipper_length_mm）和种类（species）两项数据用于后续演示：

library(tidyverse)

dat <- penguins %>%
  select(species, flipper_length_mm)

summary(dat)

##       species    flipper_length_mm
##  Adelie   :152   Min.   :172.0  
##  Chinstrap: 68   1st Qu.:190.0  
##  Gentoo   :124   Median :197.0  
##                  Mean   :200.9  
##                  3rd Qu.:213.0  
##                  Max.   :231.0  
##                  NA's   :2

根据上表可以看到

• 鳍长范围在172 - 231 mm之间，平均长度为200.9 mm；
• Adelie、Chinstrap以及Gentoo分别有152、68以及124只。

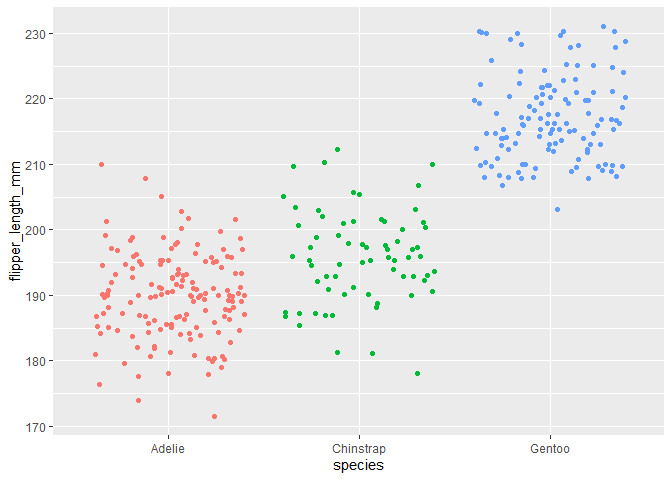
library(ggplot2)

ggplot(dat) +
  aes(x = species, y = flipper_length_mm, color = species) +
  geom_jitter() +
  theme(legend.position = "none")

目的

在本文中我们将使用方差分析来回答“三种企鹅的鳍长是否不同？”这个问题。

方差分析的原假设和备择假设分别为：

• H0 : μAdelie = μChinstrap = μGentoo（三个物种的鳍长相同）
• H1 : 至少有一个均值不同（至少有一个物种的鳍长不同于其他物种）

注意备择假设并不是所有均值都不相同，原假设（H0）的对立面应该是至少有一个均值不同于其他均值（H1）。

在这个基础上如果原假设被拒绝，那么表明至少有一个均值不同于其他两个均值，但不一定三个均值均不相同。

可能是Adelie的鳍长不同于Chinstrap和Gentoo的鳍长，而Chinstrap和Gentoo的鳍长则是相同的；可以通过事后检验来具体分析三个物种鳍长之间的差异。

基本假设

统计检验的执行需要满足假设前提，当假设不能满足时，在技术上可以执行统计检验，但解释结果并相信结论是不正确的。

变量类型

方差分析需要一个连续的定量因变量（与问题相关的测量结果相对应）和一个定性自变量（至少有两个水平）的混合。

因变量 flipper_length_mm是一个定量变量，而自变量 species是一个定性变量（三个物种），所以我们混合了两种类型的变量，并满足了该假设。

独立性

独立性的假设通常基于实验的设计和对实验条件的良好控制来实现，而不是通过形式化的测试来验证的。

由于数据是从随机选择的种群中收集的，因此假定观测结果是独立的，且三个样本组合和组间的测量结果是不相关的。

也可以通过Durbin-Watson test（durbinWatsonTest(res_lm)，res_lm是线性模型）来检验数据是否符合独立性。这个检验的原假设是指定一个自相关系数=0，而备择假设指定一个自相关系数≠0。

正态性

• 在小样本的情况下，残差应符合正态分布。可以通过直方图和Q-Q图直观的检验正态性假设；也可以使用正态性检验（如Shapiro-Wilk或Kolmogorov-Smirnov test）。如果数据经过转换（如对数变换，平方根，幂变换等），残差仍然不符合正态分布，则可使用Kruskal-Wallis test（kruskal.test(variable ~ group, data = dat）。
• 在大样本的情况下，根据中心极限定理，即使数据不符合正态分布，大样本的均值通常也近似呈正态分布。因此当样本的数据量很大（通常≥30）时，不需要检验正态假设。

由于每个物种的最小样本量是68，因此不需要检验正态性，通常会直接检验方差同质性。在本文中分别使用以下两种方法来进行正态性检验：

图形化：

在检验正态性之前，需要先计算ANOVA，并将结果保存在 res_aov中：

res_aov <- aov(flipper_length_mm ~ species,
  data = dat
)

然后可以通过直方图或Q-Q图直观的进行检验：

par(mfrow = c(1, 2)) # combine plots

# histogram
hist(res_aov$residuals)

# QQ-plot
library(car)

## 载入需要的程辑包：carData

## 
## 载入程辑包：'car'

## The following object is masked from 'package:dplyr':
## 
##     recode

## The following object is masked from 'package:purrr':
## 
##     some

qqPlot(res_aov$residuals,
  id = FALSE # id = FALSE to remove point identification
)

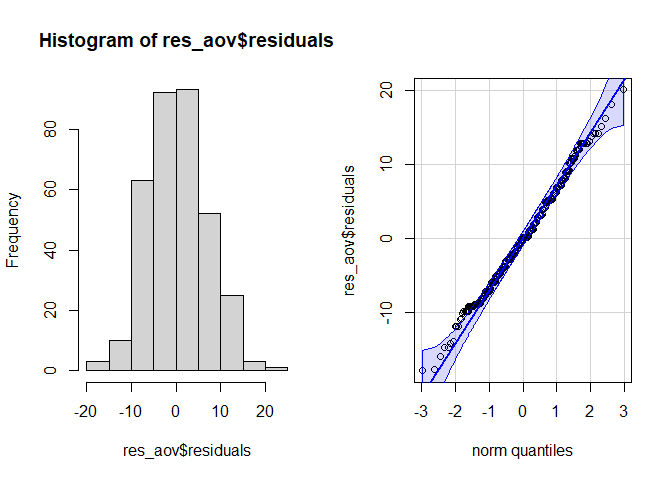
通过上面的直方图和Q-Q图，可以看到数据符合正态性。直方图大致形成一条钟形曲线，表明残差遵循正态分布。Q-Q图中的点大致沿着直线走，而且大多数都在置信区间内，这也表明残差近似遵循正态分布。

Shapiro-Wilk test：

使用Shapiro-Wilk test（或Kolmogorov-Smirnov test）来检验正态性的原假设和备择假设分别为：

• H0 : 数据来自正态分布
• H1 : 数据不是来自正态分布

shapiro.test(res_aov$residuals)

## 
##  Shapiro-Wilk normality test
## 
## data:  res_aov$residuals
## W = 0.99452, p-value = 0.2609

结果发现P＞0.05，因此接受原假设，即数据来自正态分布。

正态性假设也可以在原始数据（即观测数据）上进行检验，但是如果在原始数据上进行正态性检验，则需要分别对每个组进行正态性检验，因为方差分析要求每个组的数据都符合正态性；而对所有数据的残差或每组数据的残差分别进行正态性检验，所得到的结果是相同的。实际上“原始数据在每个组中的分布是正态分布的”就等同于说“残差是正态分布的”。

在ANOVA中实际上有两种正态性检验方法：

• 分别检验每组原始数据的正态性
• 检验所有残差的正态性（但不是每组）

在实际中使用残差进行检验会更加方便，特别是如果你有很多组或者每组只有很少的观察结果。

方差同质性

不同组的方差在总体上应该是相等的，这个假设可以通过图形化的方式进行检验（如通过比较箱线图或点线图中的离散度），也可以使用Levene’s test（使用 car包中的 leveneTest(variable ~ group)）和Bartlett test进行方差同质性检验。

如果数据不符合方差同质性的假设，则可以使用Welch ANOVA（oneway.test(variable ~ group, var.equal = FALSE)）。Welch ANOVA不要求数据满足方差同质性，但数据应符合正态分布。

如果数据不符合正态性和方差同质性，则可使用非参数检验（Kruskal-Wallis test）。

假设数据符合正态分布，接下来可以使用箱线图或点线图来检验数据方差是否符合齐性：

# Boxplot
boxplot(flipper_length_mm ~ species,
  data = dat
)

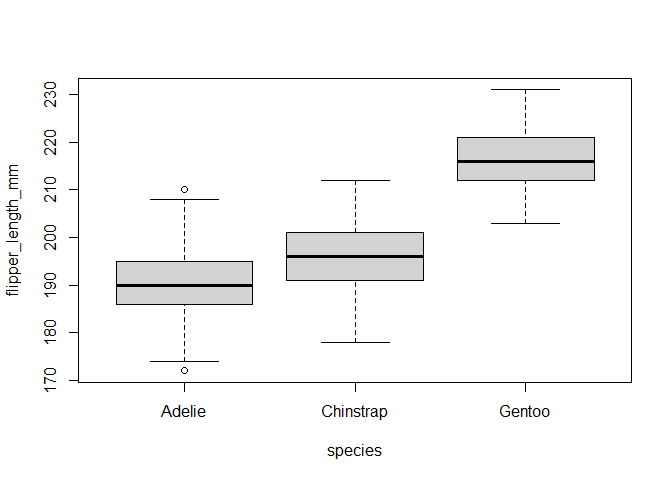
# Dotplot
library("lattice")

dotplot(flipper_length_mm ~ species,
  data = dat
)

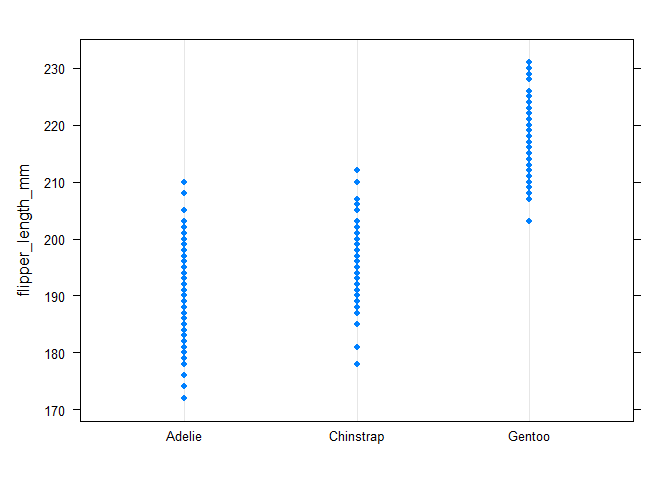
从箱线图和点线图中均可以发现不同的物种表现出相似的变异。

或者使用Levene’s test和Bartlett’s test来检验方差同质性。Levene’s test对偏离正态分布的敏感性要低于Bartlett’s test。

这两个检验的原假设和备择假设是：

• 方差相等
• 至少有一个方差是不同的

在R中可以通过 car包中的 leveneTest()函数执行Levene’s test：

# Levene's test
library(car)

leveneTest(flipper_length_mm ~ species,
  data = dat
)

## Levene's Test for Homogeneity of Variance (center = median)
##        Df F value Pr(>F)
## group   2  0.3306 0.7188
##       339

结果发现p＞0.05，所以不能排除物种间方差相等的假设，因此数据符合方差同质性。

检验正态性和方差同质性的另一种方法

可以通过 plot()函数同时检验方差齐性和残差正态性

par(mfrow = c(1, 2)) # combine plots

# 1. Homogeneity of variances
plot(res_aov, which = 3)

# 2. Normality
plot(res_aov, which = 2)

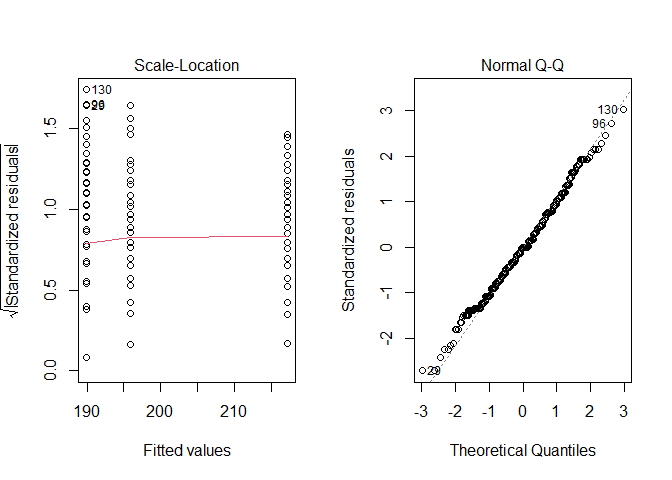
左边的图表显示，残差与拟合值（每组的平均值）之间没有明显的关系，表明各组方差相等。如果方差不同，则红线就不会是水平的。

右边的图表显示，残差基本上遵循正态分布。如果参数不符合正态性，则点将始终偏离虚线。

异常值

异常值是一个远离其他观测值的值。不同组别间应没有明显的异常值，否则方差分析的结论可能有缺陷。

通常使用箱线图来直观的对异常值进行处理：

boxplot(flipper_length_mm ~ species,
  data = dat
)

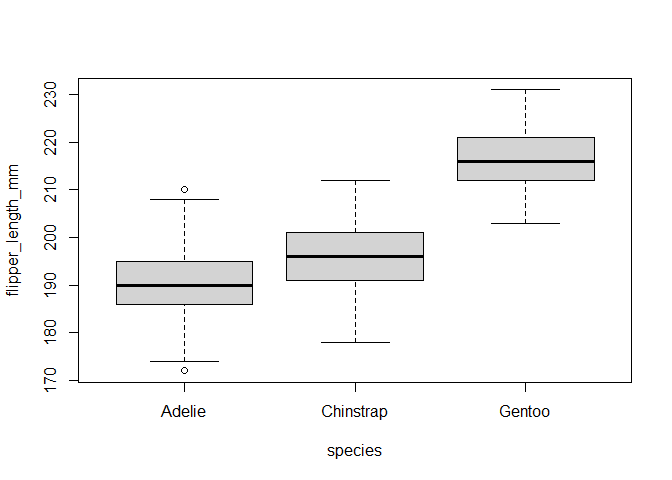
根据四分位数的定义，Adelie组中有一个异常值，然而该点并不被视为一个重要的异常值，因此可以假设数据没有重要的异常值。

小结

为了处理基本假设的这些问题，可以选择：

• 使用非参数检验
• 数据转换
• 剔除异常值（！）

下面是根据假设是否满足来选择合适的检验的总结：

1. 检查样本是否独立
2. 样本大小

• 如果样本量少，则检验残差是否符合正态分布：

  • 如果符合正态性，则检验方差齐性：

    • 如果符合方差齐性，则使用ANOVA。
    • 如果不符合方差齐性，则使用Welch ANOVA。

  • 如果不符合正态性，则使用Kruskal-Wallis test。

• 在大样本正态假设的情况下，则检验方差齐性：

  • 如果符合方差齐性，则使用ANOVA。
  • 如果不符合方差齐性，则使用Welch ANOVA。

one-way ANOVA

根据上述内容可以发现数据满足了方差分析所需要满足的假设前提，因此我们可以在R中实现方差分析，但应做一些初步分析，以至于更好的理解研究问题。

初步分析

在R中实际执行ANOVA之前，将与研究问题相关的数据可视化是一个较好的方法：

boxplot(flipper_length_mm ~ species,
  data = dat
)

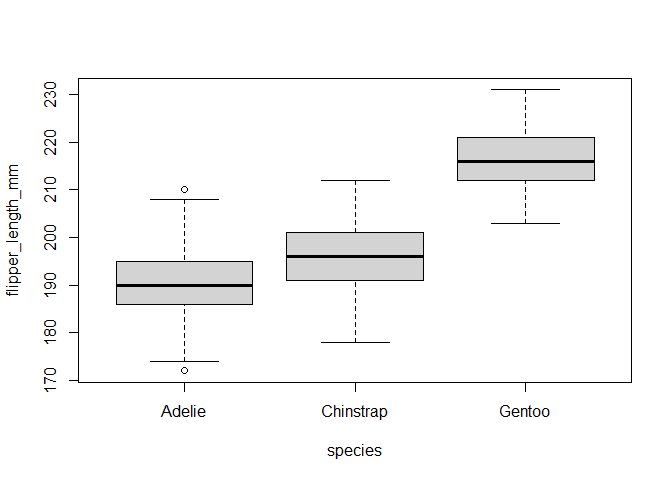
通过箱线图发现Gentoo的鳍长最大，而Adelie的鳍长则最小。

除了每个物种的箱线图外，计算一些描述统计学（例如按物种分列的平均值和标准差）也是一个不错的做法。

library(dplyr)

group_by(dat, species) %>%
  summarise(
    mean = mean(flipper_length_mm, na.rm = TRUE),
    sd = sd(flipper_length_mm, na.rm = TRUE)
  )

## # A tibble: 3 × 3
##   species    mean    sd
##   <fct>     <dbl> <dbl>
## 1 Adelie     190.  6.54
## 2 Chinstrap  196.  7.13
## 3 Gentoo     217.  6.48

鳍长的平均值也是Adelie最小，Gentoo最大。然而箱形图和描述统计学数据并不足以得出鳍长在三个种群的企鹅中存在显著差异的结论，需要进一步进行方差分析来探讨这个问题：

在R中进行方差分析

R中的方差分析可以用几种方法进行，其中两种方法如下:

1. 使用 oneway.test()函数：

# 1st method:
oneway.test(flipper_length_mm ~ species,
  data = dat,
  var.equal = TRUE # assuming equal variances
)

## 
##  One-way analysis of means
## 
## data:  flipper_length_mm and species
## F = 594.8, num df = 2, denom df = 339, p-value < 2.2e-16

1. 使用 summary()和 aov()函数：

# 2nd method:
res_aov <- aov(flipper_length_mm ~ species,
  data = dat
)

summary(res_aov)

##              Df Sum Sq Mean Sq F value Pr(>F)  
## species       2  52473   26237   594.8 <2e-16 ***
## Residuals   339  14953      44   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 因为不存在，2个观察量被删除了

从上述的两个输出结果可以看出两个方法的检验统计量（第一个方法中的F=，第二个方法中的F值）和p值（第一个方法中的p值和第二个方法中的Pr（>F））是完全相同的。因此在方差相等的情况下，结果将保持不变。

第一种方法的优点：

从ANOVA（当方差相等时使用）切换到Welch ANOVA（当方差不等时使用）比较简单方便，可以将 var.equals = TRUE替换为 var.equals = FALSE来实现，如下所示:

oneway.test(flipper_length_mm ~ species,
  data = dat,
  var.equal = FALSE # assuming unequal variances
)

## 
##  One-way analysis of means (not assuming equal variances)
## 
## data:  flipper_length_mm and species
## F = 614.01, num df = 2.00, denom df = 172.76, p-value < 2.2e-16

第二种方法的优点：

• 展示完整的方差分析表；
• ANOVA的结果（res_aov）可以保存使用，便于进行后续分析。

方差分析结果的解释

根据上述结果我们发现p＜0.05，因此我们拒绝所有平均值相等的假设，所以我们可以得出结论：至少有一个物种的鳍长不同于其他物种的鳍长。

在R中报告ANOVA结果的可以使用 report包中的 report()函数:

# install.packages("remotes")
# remotes::install_github("easystats/report") # You only need to do that once
library(report) # Load the package every time you start R

report(res_aov)

## The ANOVA (formula: flipper_length_mm ~ species) suggests that:
## 
##   - The main effect of species is statistically significant and large (F(2, 339)
## = 594.80, p < .001; Eta2 = 0.78, 95% CI [0.75, 1.00])
## 
## Effect sizes were labelled following Field's (2013) recommendations.

report()函数也可以用于其他分析。

事后检验

多重检验问题

为了研究所有组别两两之间是否具有差异，我们需要对所有组进行两两比较。由于有三个物种，我们将按以下方式进行比较：

• Chinstrap versus Adelie
• Gentoo vs. Adelie
• Gentoo vs. Chinstrap

因为我们是比较两组，理论上可以通过3个t-test来进行比较，在这种情况下t-test也是比较精确的；然而如果比较所有的组别，比较的次数也会随之剧增，这样会导致以下问题出现：

• 检验过程繁琐
• 无统一的试验误差，误差估计的精确性和检验的灵敏度低
• 推断的可靠性降低，犯α错误的概率增加

事后检验考虑到多个检验已经完成，并通过调整α来处理问题，这样至少观察到一个重要结果的概率仍然低于我们所期望的水平。

在R中进行事后检验及解释结果

几种最常见的事后检验如下:

• Tukey HSD，用于相互比较所有组。
• Dunnett，用于与参照组进行比较。例如，考虑2个处理组和一个对照组。如果你只想比较两个处理组相对于对照组，并且你不想比较两个处理组相互之间，Dunnett test是首选的。
• Bonferroni correction，只需要用比较的数量除以所需的全局α水平。在我们的例子中，我们有3个比较，所以如果我们想保持一个全局α=0.05，将得到α’= 0.05/3 = 0.0167。然后我们可以简单地对每个比较执行一个t-test，并将P值同新的α’进行比较。

Tukey HSD test

在我们的例子中，由于没有“参考”物种，并且我们有兴趣比较所有物种，我们将使用Tukey HSD test。

# Tukey HSD test:
post_test <- glht(res_aov,
  linfct = mcp(species = "Tukey")
)

summary(post_test)

## 
##   Simultaneous Tests for General Linear Hypotheses
## 
## Multiple Comparisons of Means: Tukey Contrasts
## 
## 
## Fit: aov(formula = flipper_length_mm ~ species, data = dat)
## 
## Linear Hypotheses:
##                         Estimate Std. Error t value Pr(>|t|)  
## Chinstrap - Adelie == 0   5.8699     0.9699   6.052   <1e-08 ***
## Gentoo - Adelie == 0     27.2333     0.8067  33.760   <1e-08 ***
## Gentoo - Chinstrap == 0  21.3635     1.0036  21.286   <1e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)

在Tukey HSD test的输出中，在表的第一列显示了已经进行的比较，最后一列(Pr(>|t|))显示了每次比较的调整后的p值（原假设为两组相等，备择假设为两组不同），正是这些调整后的p值用于检验两组是否存在显著差异。

在这个例子中进行了如下检验:

• Chinstrap versus Adelie (line Chinstrap - Adelie == 0)
• Gentoo vs. Adelie (line Gentoo - Adelie == 0)
• Gentoo vs. Chinstrap (line Gentoo - Chinstrap == 0)

结果发现p值都小于0.05，因此我们拒绝所有比较的零假设，表明所有物种的鳍长存在显著差异。

事后检验的结果可以通过 plot()函数来显示:

par(mar = c(3, 8, 3, 3))
plot(post_test)

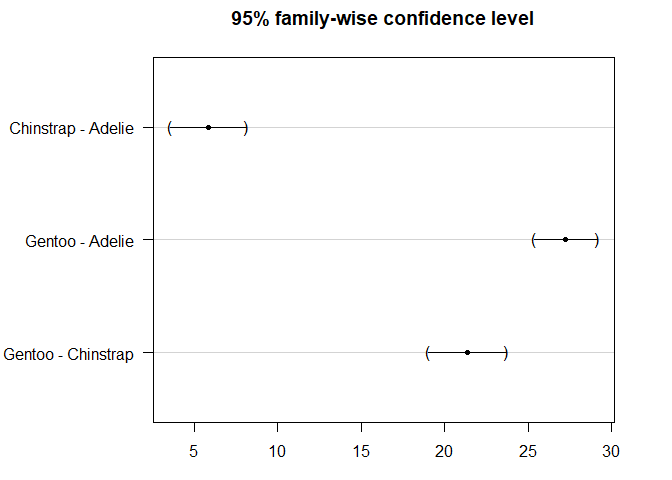
置信区间并没有跨越零线，这表明所有的物种的鳍长存在显著差异。

TukeyHSD test也可以用 TukeyHSD()函数完成:

TukeyHSD(res_aov)

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = flipper_length_mm ~ species, data = dat)
## 
## $species
##                       diff       lwr       upr p adj
## Chinstrap-Adelie  5.869887  3.586583  8.153191     0
## Gentoo-Adelie    27.233349 25.334376 29.132323     0
## Gentoo-Chinstrap 21.363462 19.000841 23.726084     0

结果也可以通过 plot()函数来可视化：

plot(TukeyHSD(res_aov))

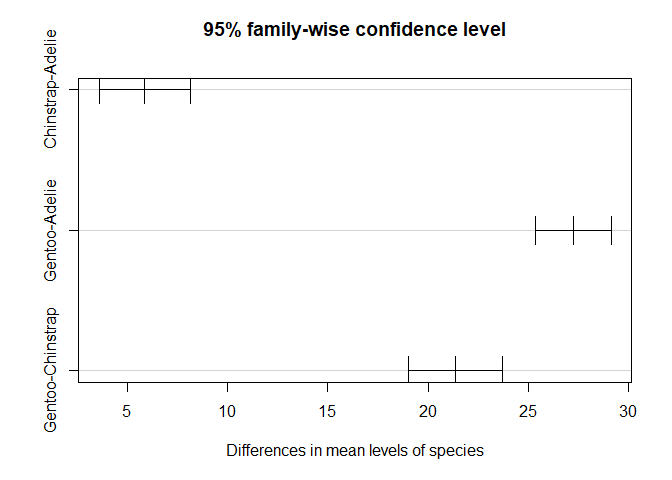
Dunnett’s test

将所有可能的组与Tukey HSD test进行比较是一种常见的方法，但许多研究都有一个对照组和几个处理组。对于这些研究可能只需要比较对照组和处理组，这样就减少了比较的次数。

Dunnett’s test将处理组同对照组进行比较，而不是将所有组彼此进行比较。

现在以Adelie作为对照物种，只比较对照物种和其他两个物种：

Dunnett’s test与Tukey HSD test的区别在于 linfct = mcp(species = "Dunnett"):

library(multcomp)

# Dunnett's test:
post_test <- glht(res_aov,
  linfct = mcp(species = "Dunnett")
)

summary(post_test)

## 
##   Simultaneous Tests for General Linear Hypotheses
## 
## Multiple Comparisons of Means: Dunnett Contrasts
## 
## 
## Fit: aov(formula = flipper_length_mm ~ species, data = dat)
## 
## Linear Hypotheses:
##                         Estimate Std. Error t value Pr(>|t|)  
## Chinstrap - Adelie == 0   5.8699     0.9699   6.052 7.59e-09 ***
## Gentoo - Adelie == 0     27.2333     0.8067  33.760  < 1e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)

事后检验的结果同样可以用 plot()函数展示：

par(mar = c(3, 8, 3, 3))
plot(post_test)

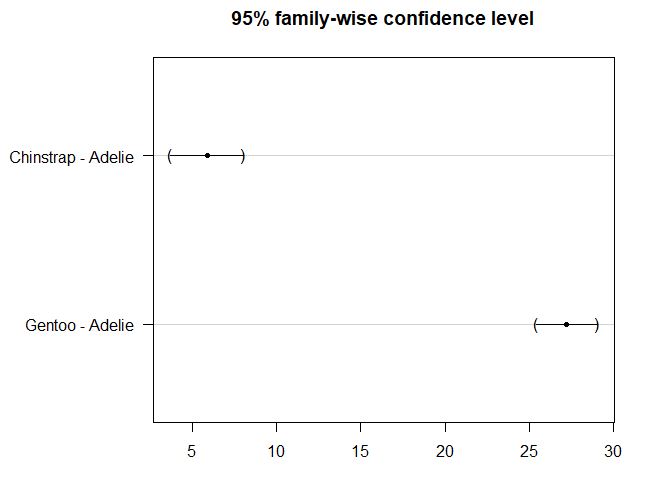
默认情况下，因子变量的引用类别是字母顺序中的第一个类别。这就是为什么在默认情况下，参考物种是Adelie。引用类别可以通过 relevel ()函数（或通过 {questionr} addin）更改。现在我们希望以Gentoo作为对照物种，而不是以Adelie作为对照：

# Change reference category:
dat$species <- relevel(dat$species, ref = "Gentoo")

# Check that Gentoo is the reference category:
levels(dat$species)

## [1] "Gentoo"    "Adelie"    "Chinstrap"

Gentoo现在是实际上被作为对照物种的类别：

为了使用新的参考进行Dunnett’s test，需要重新计算ANOVA:

res_aov2 <- aov(flipper_length_mm ~ species,
  data = dat
)

然后我们可以用方差分析的新结果进行Dunnett’s test:

# Dunnett's test:
post_test <- glht(res_aov2,
  linfct = mcp(species = "Dunnett")
)

summary(post_test)

## 
##   Simultaneous Tests for General Linear Hypotheses
## 
## Multiple Comparisons of Means: Dunnett Contrasts
## 
## 
## Fit: aov(formula = flipper_length_mm ~ species, data = dat)
## 
## Linear Hypotheses:
##                         Estimate Std. Error t value Pr(>|t|)  
## Adelie - Gentoo == 0    -27.2333     0.8067  -33.76   <1e-10 ***
## Chinstrap - Gentoo == 0 -21.3635     1.0036  -21.29   <1e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)

par(mar = c(3, 8, 3, 3))
plot(post_test)

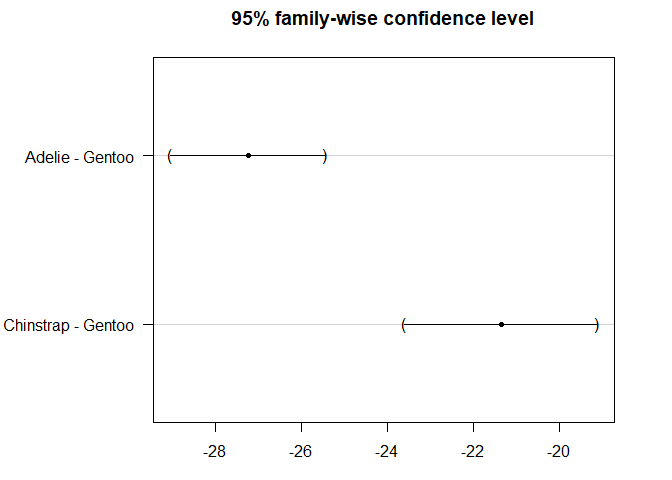
可视化

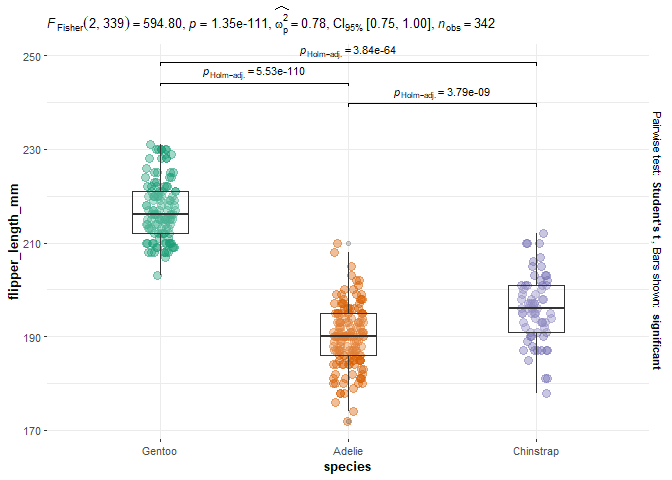
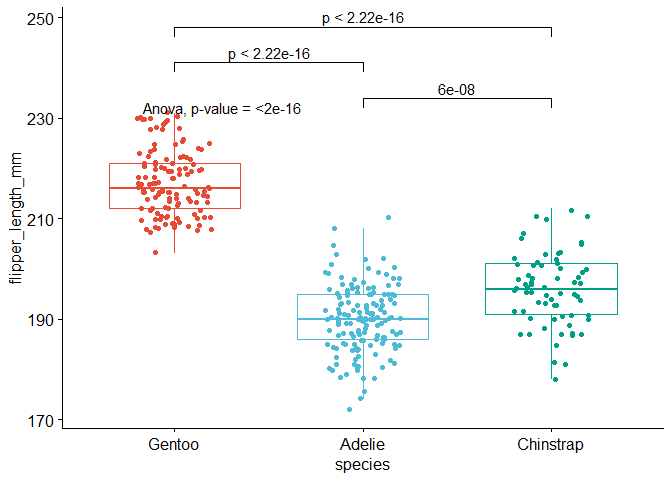
以下是两段对方差分析及事后检验进行可视化的代码

# Edit from here
x <- which(names(dat) == "species") # name of grouping variable
y <- which(
  names(dat) == "flipper_length_mm" # names of variables to test
)
method1 <- "anova" # one of "anova" or "kruskal.test"
method2 <- "t.test" # one of "wilcox.test" or "t.test"
my_comparisons <- list(c("Chinstrap", "Adelie"), c("Gentoo", "Adelie"), c("Gentoo", "Chinstrap")) # comparisons for post-hoc tests
# Edit until here


# Edit at your own risk
library(ggpubr)
for (i in y) {
  for (j in x) {
    p <- ggboxplot(dat,
      x = colnames(dat[j]), y = colnames(dat[i]),
      color = colnames(dat[j]),
      legend = "none",
      palette = "npg",
      add = "jitter"
    )
    print(
      p + stat_compare_means(aes(label = paste0(after_stat(method), ", p-value = ", after_stat(p.format))),
        method = method1, label.y = max(dat[, i], na.rm = TRUE)
      )
      + stat_compare_means(comparisons = my_comparisons, method = method2, label = "p.format") # remove if p-value of ANOVA or Kruskal-Wallis test >= alpha
    )
  }
}

第二个方法来自 {ggstatsplot}包:

library(ggstatsplot)

ggbetweenstats(
  data = dat,
  x = species,
  y = flipper_length_mm,
  type = "parametric", # ANOVA or Kruskal-Wallis
  var.equal = TRUE, # ANOVA or Welch ANOVA
  plot.type = "box",
  pairwise.comparisons = TRUE,
  pairwise.display = "significant",
  centrality.plotting = FALSE,
  bf.message = FALSE
)